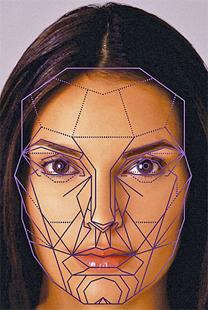
लाइनों की पूर्णता - जीवन में अक्षीय समरूपता

प्राचीन काल से मनुष्य ने प्रतिनिधित्व किया हैसौंदर्य के बारे में प्रकृति के सभी प्राणी सुंदर हैं अपने तरीके से, लोग सुंदर हैं, जानवरों और पौधों अद्भुत हैं एक बहुमूल्य पत्थर या नमक क्रिस्टल की दृष्टि को पसंद करते हैं, यह हिमपात या बटरफ़्लाइ का आनंद नहीं लेना मुश्किल है लेकिन ऐसा क्यों होता है? हम सही और ऑब्जेक्ट्स की तरह लगते हैं, जिनमें से दाएं और बायां आधा दर्पण छवि में दिखते हैं।

जाहिर है, पहले लोगों को सौंदर्य के सार के बारे में सोचने के लिएकला। प्राचीन मूर्तिकार जो मानव शरीर की संरचना का अध्ययन करते थे, वापस वी सदी ईसा पूर्व में थे "समरूपता" की अवधारणा को लागू करना शुरू कर दिया यह शब्द ग्रीक मूल का है और इसका मतलब सामंजस्य, आनुपातिकता और घटक भागों के स्थान की समानता है। प्राचीन ग्रीस के दार्शनिक प्लेटो ने तर्क दिया कि जो सुंदर हो सकता है वह सममित और आनुपातिक है।

ज्यामिति और गणित में तीन प्रकार की समरूपता समझाई जाती है: अक्षीय समरूपता (एक सीधी रेखा के संबंध में), मध्य (एक बिंदु के संबंध में) और दर्पण (विमान के संबंध में)।

अगर वस्तु के प्रत्येक अंक के भीतर हैइसके केंद्र के संबंध में इसका अपना सही नक्शा है - एक केंद्रीय समरूपता है इसका उदाहरण ऐसे ज्यामितीय निकाय हैं जैसे कि सिलेंडर, एक बॉल, नियमित चश्मे आदि।

सीधी रेखा के संबंध में अंकों की अक्षीय समरूपताप्रदान करता है कि यह सीधी रेखा सेगमेंट के बीच के बिंदुओं को पार करती है, और यह उसके लिए लंबवत है। समरूपता के अक्ष के उदाहरण: एक समद्विबाहु त्रिकोण के बिना विस्तारित कोण के द्विभाजक, किसी भी सीधी रेखा को एक वृत्त के केंद्र के माध्यम से खींचा जाता है, आदि। यदि ज्यामितीय आकृति की अक्षीय समरूपता की विशेषता होती है, तो दर्पण बिंदु की परिभाषा को केवल धुरी के साथ झुका करके और समान भाग को चेहरे से जोड़कर देखा जा सकता है। आवश्यक अंक संपर्क में एक ही समय में आएंगे।

दर्पण समरूपता के साथ, ऑब्जेक्ट के अंक समान केंद्र से संबंधित होते हैं जो उसके केंद्र से गुजरता है।

प्रकृति बुद्धिमान और तर्कसंगत है, इसलिए लगभग सभी इसेकृतियों में एक सामंजस्यपूर्ण संरचना है यह जीवित प्राणियों पर लागू होता है, और निर्जीव वस्तुओं के लिए। जीवन के अधिकतर रूपों की संरचना के लिए, तीन प्रकार के समरूपता में से एक विशेषता है: दो तरफा, किरण या गोलाकार

प्रायः अक्षीय समरूपता प्रकृति में कर सकते हैंमिट्टी की सतह के लिए लंबवत विकसित पौधों में देखा गया। इस मामले में, समरूपता केंद्र में स्थित सामान्य अक्ष के आस-पास समान तत्वों के रोटेशन का परिणाम है। उनके स्थान के कोण और आवृत्ति अलग-अलग हो सकते हैं। उदाहरण पेड़ हैं: स्प्रूस, मेपल और अन्य। कुछ जानवरों में, अक्षीय समरूपता भी होती है, लेकिन यह अक्सर कम होता है बेशक, प्रकृति को शायद ही कभी गणितीय सटीकता की विशेषता है, लेकिन शरीर के तत्वों की समानता अभी भी आश्चर्यजनक है।

जीवविज्ञान अक्सर गैर-अक्षीय रूप से विचार करते हैंसममिति, और द्विपक्षीय (द्विपक्षीय) उनका उदाहरण एक तितली या डैगनफ़्लू के पंख, पौधे, फूलों की पंखुड़ियों आदि के पत्ते हैं। प्रत्येक मामले में, जीवित वस्तु के दाएं और बाएं हिस्से समान होते हैं और एक दूसरे की एक दर्पण छवि का प्रतिनिधित्व करते हैं।

गोलाकार समरूपता कई पौधों के फल की विशेषता है, कुछ मछलियों, मॉलस्क और वायरस के लिए। रे समरूपता के उदाहरणों में स्टारफ़िश, कीड़े, ईचिनोडर्म की कुछ प्रजातियां हैं।

किसी व्यक्ति की आंखों में, असमंजसता अक्सर अनुचित या दोषपूर्ण व्यवहार से जुड़ा होता है। इसलिए, मानव हाथों की अधिकांश रचनाओं में, समरूपता और सद्भाव का पता लगाया जाता है।

</ p>